Beam elements
- Is a slender structure in which the length is isgnificantly larger than the other two dimensions. A beam element is a one-dimensional line or curve that represents the neutral axis of the beam.
- The stress in the direction of the beam element (the bending stress) is considered significantly greater than other stresses.
- Allowed to only deform in the transverse direction
- The loads applied are specified as shear forces and bending moments
- 2 degrees of freedom per node: transverse (normal) displacement and rotation about the neutral axis. The rotation is the derivative of transverse displacement
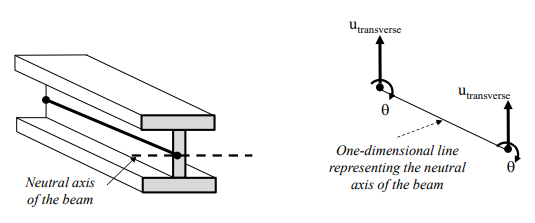
- Different with pin-jointed elements. PJE has only nodal displacement as degree of freedom. PJE can only stretch or compress along the line of the element.
Two assumptions for the beam thickness:
- Thin beam elements (Euler-Bernoulli formulations): shear deformations are ignored plane cross sections remain perpendicular after deformation
- Thick beam element (Timoshenko formulations): sear deformations are allowed, cross-section may not remain normal

- The external force vector contains the shear loads and the bending moment
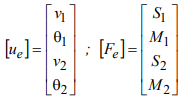
- Theta is the slope of the transverse displacement at the nodal point
- To model continous beam structure, theta must be continue from one beam element to another. So, displacement must be at least cubic interpolation
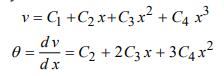
Created with the Personal Edition of HelpNDoc: Easy EBook and documentation generator